1 Topic by c.wilson4

  • c.wilson4
  • Member
  • Offline

Hi, First of all thank you for this software. It is so intuitive and easy to use.

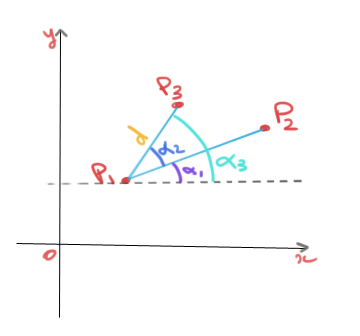
I am seeing if this software will work for my study. I am trying to track an objects position relative to a 2D plane. I would like to track its position (X,Y) but also the angle or direction the object is facing. The camera will not be directly above the plane either, so I am using a perspective grid to calibrate.

I have attached some images of a mockup I am experimenting with. I have marked the images in red so you can see the kind of measurment I need.

There could be a way of calculating it using the relative position of the 2 points in excel, but I would rather skip that step If I can.

https://i.imgur.com/EcVR71E.png

2 Reply by c.wilson4

  • c.wilson4
  • Member
  • Offline

Second image:

https://i.imgur.com/PAdjk5l.png

3 Reply by joan

  • joan
  • joan
  • Admin
  • Offline

Hi,
Unfortunately at the moment there is no way to get the angle between two disconnected segments. And there is also no way to get the angle-to-horizontal axis in the perspective calibration case.
For this second case it could be added to the line tool without too much effort. I think this could also help in another specific scenario with the goniometer tool that has been causing an issue.

4 Reply by c.wilson4

  • c.wilson4
  • Member
  • Offline

No problem, Thank you for the reply.

It should be possible to calculate it by knowing the position of 2 tracked points and the distance between them.

I will experiment a bit in Excel and see if I can work it out.

5 Reply by joan

  • joan
  • joan
  • Admin
  • Offline

Yes if you subtract the points (end - start) then you should be able to use the atan2 function to get an angle relative to the x-axis. I think Excel has such a function.

6 Reply by c.wilson4

  • c.wilson4
  • Member
  • Offline

Hi Joan,

Thank ou for your help at the start of the year.

I have implimented Kinovea for my study, ran the user trial and collected my data. When I get round to publishing results I will post on here about it as I am using the software for something quite novel.

I do have one excel/math question which I am struggling with. Using 2 tracked points (like the example above) I am trying to determine the coordinates of a 3rd "virtual point". It is fixed relative to the 2 tracked points and I know the position of both points and the angle of rotation relative to an edge (like above).

This is the formula I am currently playing with:

To calculate the Y coordinate: =Y+(42.4*SIN(((71.5*PI()/180)+(A*PI()/180))))
To calculate the X coordinate: =X+(42.4*COS(((71.5*PI()/180)+(A*PI()/180))))

Where:
Y=Tragectory 1 Y coordinate
X=Tragectory 1 X coordinate
A=angle of rotation (can be possitive and negative)

I am not sure what isn't working, but I suspect it is to do with the angle of rotation. Any help would be very much appreciated.

Kind regards,
Chris

7 Reply by c.wilson4

  • c.wilson4
  • Member
  • Offline
c.wilson4 wrote:

Hi Joan,

Thank ou for your help at the start of the year.

I have implimented Kinovea for my study, ran the user trial and collected my data. When I get round to publishing results I will post on here about it as I am using the software for something quite novel.

I do have one excel/math question which I am struggling with. Using 2 tracked points (like the example above) I am trying to determine the coordinates of a 3rd "virtual point". It is fixed relative to the 2 tracked points and I know the position of both points and the angle of rotation relative to an edge (like above).

This is the formula I am currently playing with:

To calculate the Y coordinate: =Y+(42.4*SIN(((71.5*PI()/180)+(A*PI()/180))))
To calculate the X coordinate: =X+(42.4*COS(((71.5*PI()/180)+(A*PI()/180))))

Where:
Y=Tragectory 1 Y coordinate
X=Tragectory 1 X coordinate
A=angle of rotation (can be possitive and negative)

I am not sure what isn't working, but I suspect it is to do with the angle of rotation. Any help would be very much appreciated.

Kind regards,
Chris

So I hate browsing forums that have questions without answers. This weekend I figured it out so I am posting here to maybe help people in the future.

First of all the formulas are wrong, they should be:

P3X = =P1X+((distance*(COS((angular change+internal angle)*(PI()/180)))))
P3Y = =P1Y+((distance*(COS((angular change+internal angle)*(PI()/180)))))

The second mistake I made was to use a negative version of the angle rather than the calculated.

8 Reply by joan

  • joan
  • joan
  • Admin
  • Offline

I glanced at it but didn't really find any issue, so now I'm confused by your new formula smile

Did you mean to write COS in the second line? It made more sense for the Y coordinate to be = radius * sin(angle), where "angle" is the total angle, in radians, relatively to the global X-axis and "radius" is the distance to the known point. There might be an issue in the way you compute the P1-P2 line angle relatively to the X-axis?

I made a little drawing:
https://www.kinovea.org/screencaps/relative-coords2.png

I'm assuming you are tracking P1 and P2 and you are looking for P3. And assuming you know about alpha2 (blue) (the P2-P1-P3 angle) that you measure by hand on the object, and you also know d, the distance between P1 and P3, measured on the object.

So what you are doing is, find alpha1, then compute alpha3, compute the P1-P3 vector from trigonometry, and add that vector to P1. Correct?
Your original formula should work: 

P3x = P1x + d * cos(alpha3)
P3y = P1y + d * sin(alpha3)

How do you compute alpha1?

There is another way that doesn't involve angles, if you express P3 in its own little coordinate system where P1-P2 is the horizontal unit vector.

9 Reply by c.wilson4

  • c.wilson4
  • Member
  • Offline

Alpha1 was computed using ATAN2 (as above).

Yes I wrote it wrong above, it should have been SIN instead of COS.

The orginal formula may have worked but my Alpha1 was negative rather than possitive (my fault).

I managed to make life hard for myself but it is now working fine, just need to process my 40hours of footage into coordinates now...